Let say that you have a unit Normal N in d dimensions. Then the variance is Chi-square distributed, and the standard deviation is Chi distributed. In other words, the distance between a random point drawn from N to the origin has the Chi distribution.

Now the thing is that the Chi distribution only depends on the number of dimensions of the original Normal N, and it grows ~ sqrt(d). So when the number of dimensions d grows, the points of N do not concentrate around the mean anymore, but in a space between 2 hypersphere, as you can see from the distance of the points to the center is concentrated around sqrt(d).

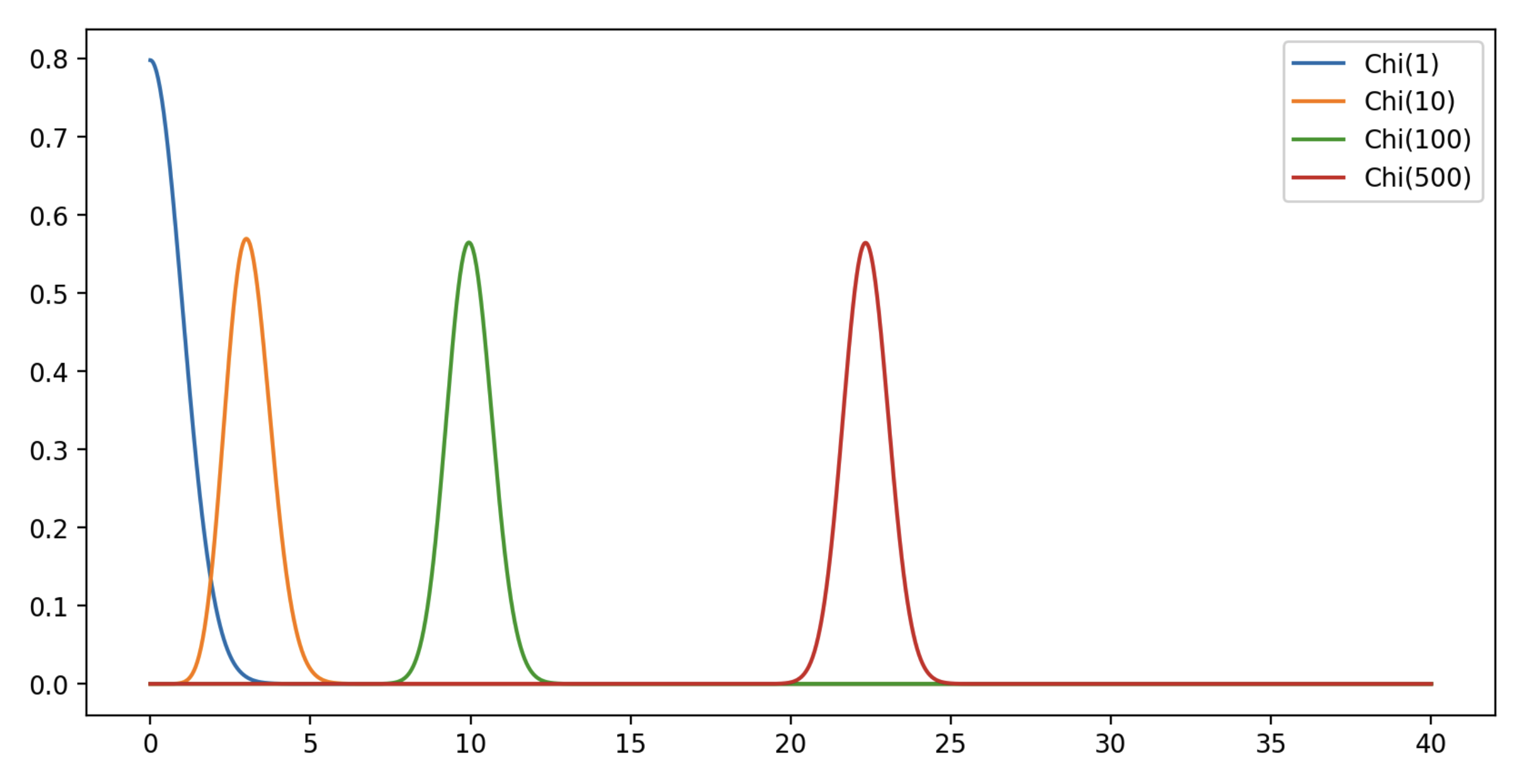
Still not convinced ? Here the plot of distance of points to the origin drawn from some unit multivariate Normal. Source

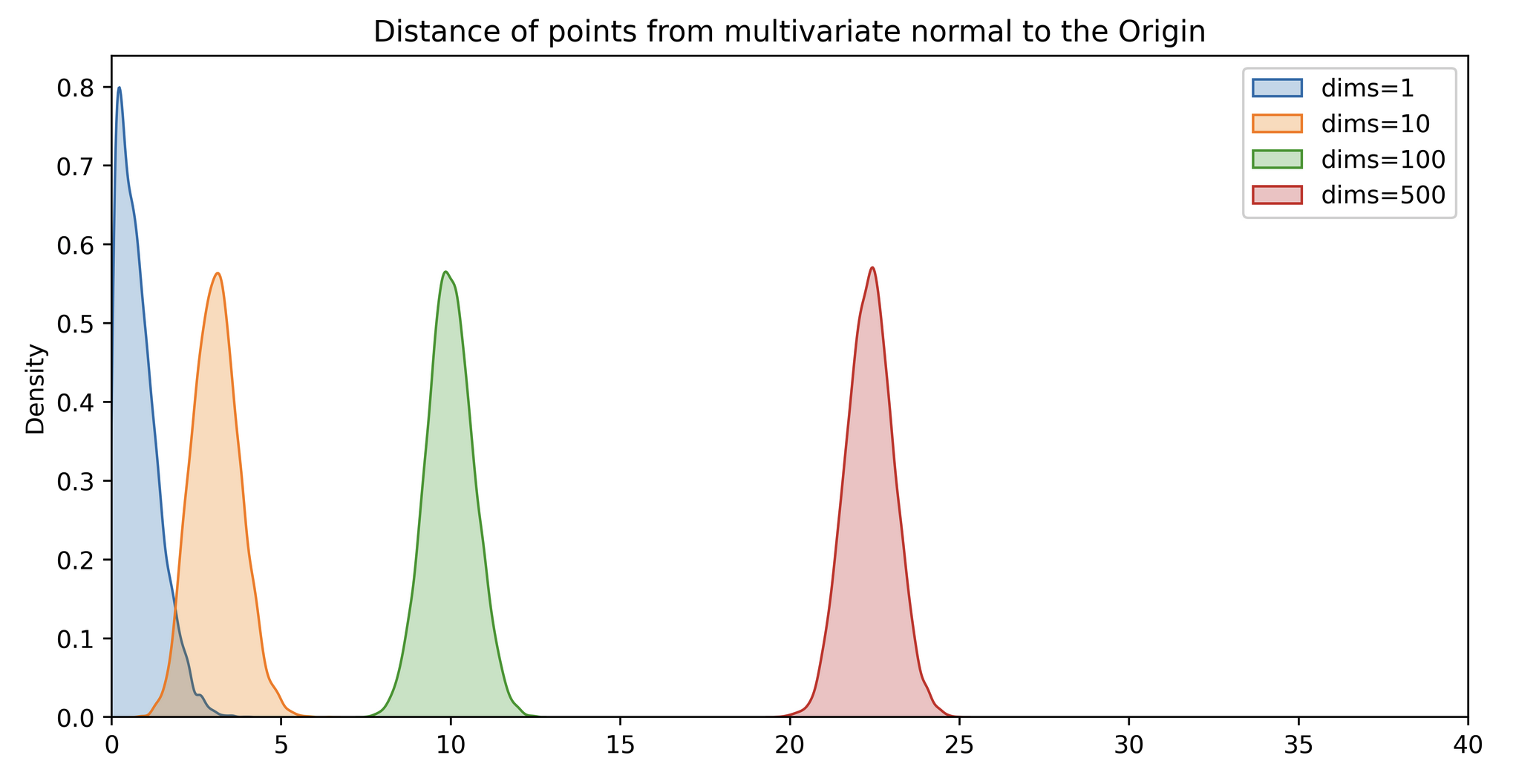
For MCMC inference, we want the chains to explore the space where the bulk of the distribution is. This region of space is called the Typical Set.

Thus, setting the initial points to MAP values is just premature optimization, and does not offer anything and even make the sampling process worse. Modern MCMC frameworks such as Pymc3 has several tricks to initialize the chain in order to reach the typical set most efficiently.