Training SVM on much smaller dataset sampled from the original, using entropy

This is part 2 of the series on using quantized space as representation of points. In the first post, we trained an SVM on quantized samples and successfully reduced the training time by orders of magnitude. In this post, we take further steps and reduce the quantized sample points to an extreme.

The idea behind training SVM on quantized sample space is that most of the influence to the decision boundary comes from points close to the decision boundary (DB) itself. Further points from the DB, the less likely it is to be important. This is the robustness of SVM.

This property is special to SVM. Other methods such as Logistic Regression (or other Gradient Descent methods ) don’t have this. It’s easily influenced by outliers.

Using Entropy

Given a distribution, entropy measures how ununiform it is. It has the least Entropy when everything is the same, and has the most entropy when everything has an equal share.

From an Information Theory perspective, entropy measures the amount of information I need to encode that distribution.

The important observation I have is that the space close to Decision Boundary has higher entropy. Thus, I can use entropy of the space around a point as a proxy to the importance of the point to the decision function. This is one of the most fundamental questions in SVM: choosing the datapoints.

Another way to look at this is how much information I lose if I throw away all the information I have about points in this cell, and encoding everything with the most popular label. The lost information amounts to the entropy.

Experiments

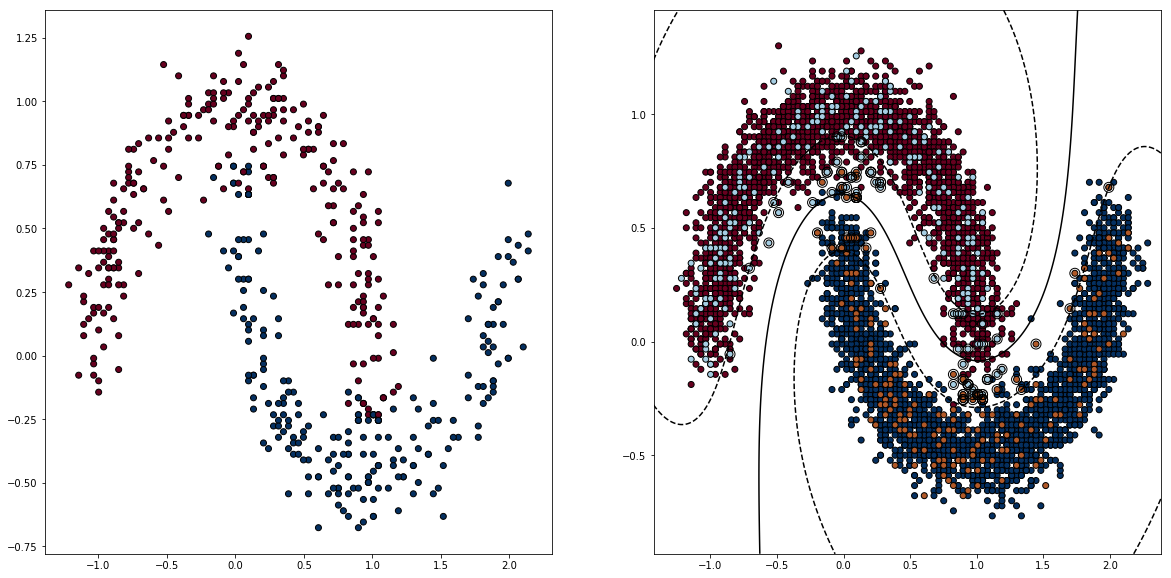
Here, we use sklearn.FeatureDiscretizer to quantize the space into a grid of cells, then resample the points based on the entropy of the cell. Higher entropy, the more likely it is being chosen. The cells with total homogeneity are assigned a small sampling probability to make sure some of the points in the middle of the points cloud are included.

SVM on 100000 points Gaussian cloud, take a long time to train

Results from the Kernel SVM with much fewer points. Here we sample 500 points out of 100000 points. THe orange and teal points are the sampled data points.

SVM on only 500 points, near the decision boundary, we can see more points are sampled.

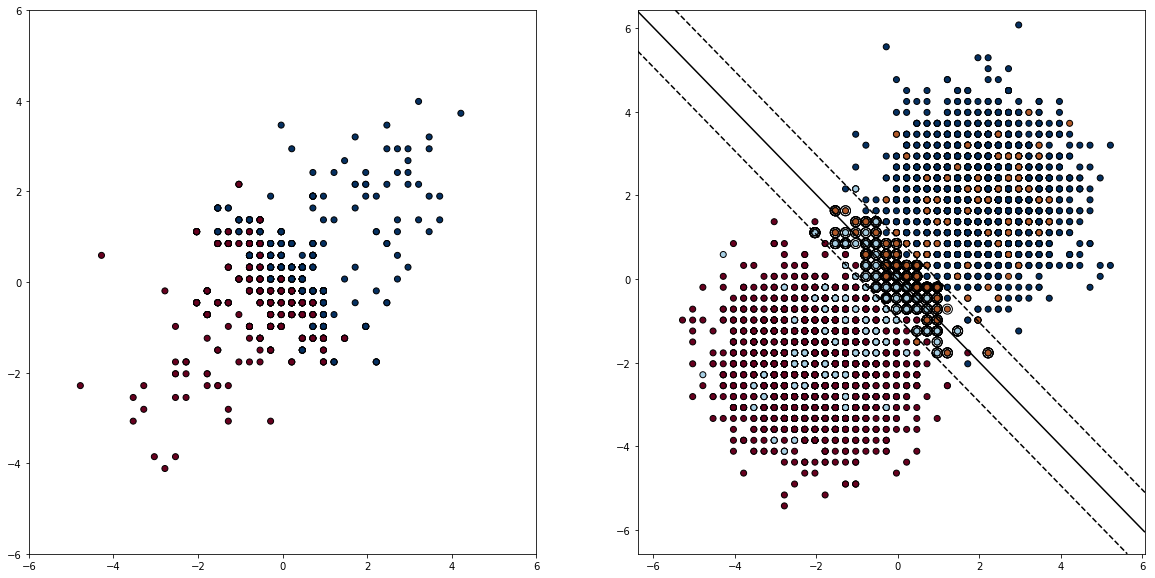
We can use NearestNeighbor method to calculate the same entropy, but it’s much more computationally expensive, given the objective is to speed up SVM.

The parameters for this method is the width of the cells and the base sampling prob and can be tuned by CV. More on that later.