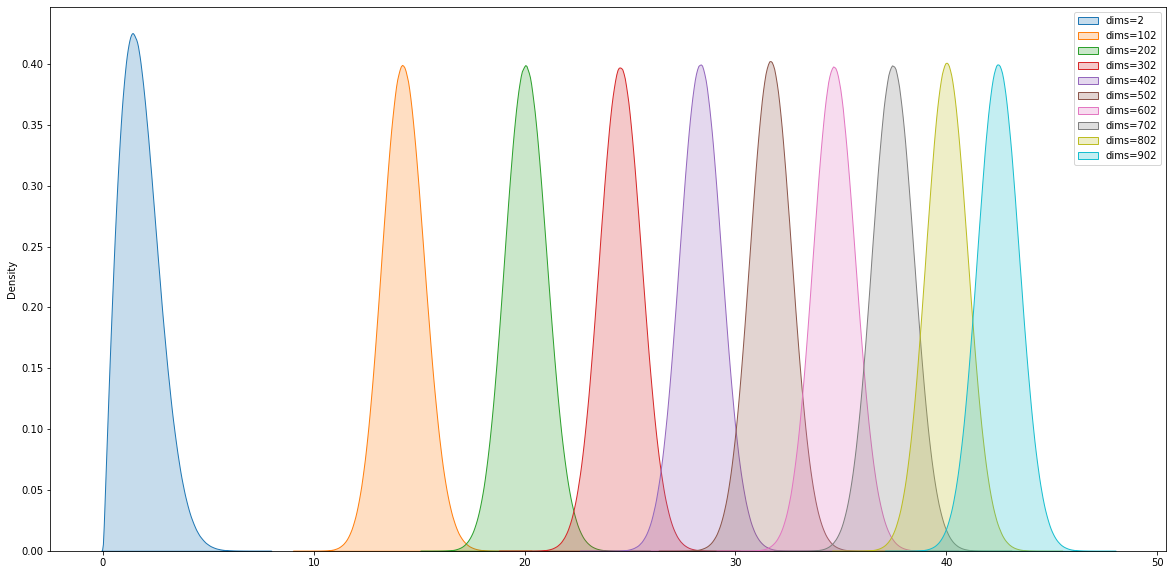
Pairwise distances between points of a Gaussian in high dim.

In the previous post, I’ve talked about why starting your MCMC chain at MAP is a bad idea, since High Dimensional space behaves very differently to what we usually imagine in low dimensions.

The core concept here is that points are squished into the Typical Set, that resembles a shell. This post demonstrates the pairwise distances between points of a Gaussian distribution in high dimension.

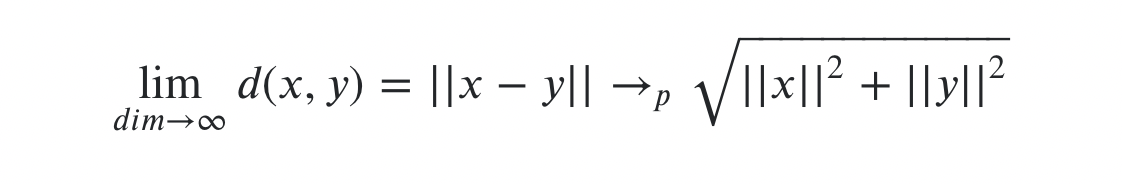
To demonstrate this point further, if we limit our points to be distributed randomly on a unit hypersphere, the pairwise distance between points will tend to sqrt(2) when the number of dimensions tends to infinity.

Reference for more research on the topic.

When the number of dimension d tends to infinity, and the points of a Gaussian dist redistribute in a shell of distance sqrt(d) around the origin. This distance grows only with the number of dimensions. One result is that the ratio of distances between the nearest point and the furthest point goes to 1 as d tends to infinity. Points of a Gaussian become uniformly spaced out.

So you see, local search methods will have a hard time to find points if all the points are equally far away of the point of interest. In practice, it usually shows up as poor performance gain when comparing to a random search when we have a moderate amount of points compare to amount of dimension ( The data is sparse comparing to the number of dimension, like text vectors for example).